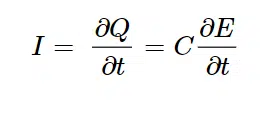The Cottrell Experiment and Diffusion Limitation 3/3 – Electrochemical Double Layer

Electrochemical double layer

As soon as an electrode surface is charged, due to a potentiostat or its Nernst potential, an electric field is created. Charged particles will move in this field. Ions of the other charge than the electrodes charge will accumulate directly at the electrode, forming a layer of ions.

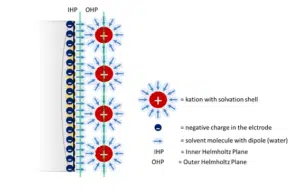
Assuming that the electrode is positive charged, anions will accumulate. Attracted by these anions, kations will be attracted and form another loose layer on top of the first layer. The first layer is known as the outer Helmholtz plane. The charges accumulating in the metal surface are the inner Helmholtz plane (see Figure 2.1). The layer of ions and the electrode act like a capacitor and this has impact on most electrochemical techniques.

This is only a rudimentary description of the electrochemical double layer; there are more sophisticated models, but for many electrochemical experiments the simple model will suffice. 

Migration

Up to now it was assumed that the electrochemical active species Red is transported by diffusion or convection only, but there is one more way for mass transport: migration. Migration is mass transport due to an electric field. If Red is negatively charged, the positive potential of the electrode will attract the Red-ions. 

Why are complete models and observations done without taking migration into consideration? Usually an electrochemical measurement is done in a well-conducting solution. Since the current flows from the working to the counter electrode through the solution, a high solution resistance will make the measured current smaller and increase the Ohmic drop (i.e. the difference in the potential applied between the reference electrode and the working electrode and the potential that the working electrode is feeling, see also Ohmic drop).

To reduce the resistance of a solution, an electrochemical inert support electrolyte is added. Often the buffer itself in a pH buffered solution is sufficient or a salt with a high solubility, for example KCl, NaCl, NaSO4, NaNO3, is added.

If the support electrolyte has a high concentration compared to the investigated species, in this example Red, the electric field will be compensated by the ions of the support electrolyte and almost only these will migrate. A rule of thumb is that the support electrolyte should have a hundred times higher concentration. Since this effect is suppressed so easily, migration is often negligible. 

Another effect is the capacitive charging current or short capacitive current. As mentioned the electrochemical double layers acts as capacitor. Capacitors store charge.

A simple capacitor is the plate capacitor. It comprises two conducting parallel plates that are not in contact with each other. If a power source is connected to the plates, a current flows that is exponentially decaying until it is insignificant. A current flows because one plate is charged negative and the other positive. The separation of charges means current flows. At some point the plates cannot store more charge and the current stops flowing. The current decays over time according to 

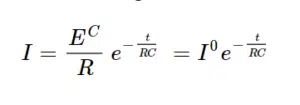
EC is the charging potential or voltage, I0 is the starting current, R is the resistance of the circuit around the capacitor, t the time and C the capacity of the capacitor. The capacity is a property of the capacitor and is defined as the charge Q that can be stored per applied potential E or as equation 

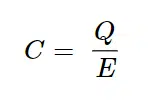
Usually U is used for voltage, but since these equations need to be transferred to electrochemical experiments, it is useful to start with the potential E instead of the voltage U. These two are not synonymous but in this context it is fine to exchange them. 

Properties of the electrochemical double layer

If it is assumed that the electrochemical double layer behaves exactly like a plate capacitor, the two equations 2.1 and 2.2 show three important facts: 

1. The capacitive current decays exponentially with the time t. The higher resistance R and capacity C are, the slower it will be decaying. The product of resistance R and capacity C is often called the time constant τ. 
2. The charge Q that can be stored is proportional to the applied potential. Every time the charge Q that can be stored changes a current I flows until the charge Q is adjusted. The charge Q that can be stored changes, if the potential E is changing. This is expressed in the equation:
   
   

   

3. In equation 2.2 it is shown implicitly and in 2.3 explicitly that the higher the capacity C is, the more capacitive current will flow if the potential changes.

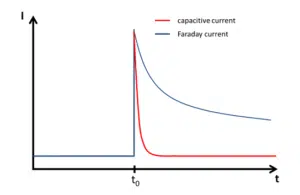
Capacitive and Faraday current

Usually electrochemists are interested in the Faraday current, that is the current caused by an electrochemical reaction; the capacitive current, caused by physics, is an unwanted side effect (see also Capacitive current).  

What does this mean for measurements? If the potential of the electrode is changed, for example during a potential step, a current will flow that has no chemical but only a physical meaning. This current decays exponential with t, while the Faraday current decays with t-½. This means that the capacitive current decays much faster than the Faraday current (see Figure 2.2). The higher the capacity C the higher the capacitive current. The capacity C for a plate capacitor can be calculated with 

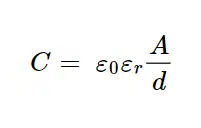
where ε0 is the electric field constant, εr is the relative permittivity of the medium between the plates, d is the distance between the two plates and A is the surface area of the two plates. 

In conclusion, most factors influencing the capacity cannot be altered in an electrochemical experiment. The constant ε0 cannot be changed. The distance d and the relative permittivity εr can only be changed by changing the solution, because d is defined by the distance between inner and outer Helmholtz plane (see Figure 2.1). The area A is influenced by the surface roughness. The rougher a surface the higher its area. If a reusable electrode is used, a proper polishing that leads to a smooth surface can reduce capacitive current drastically.