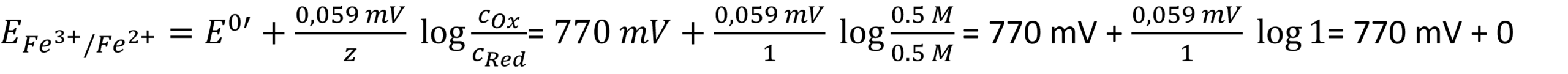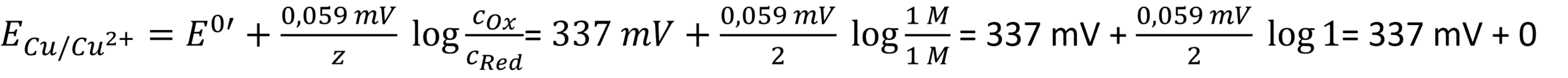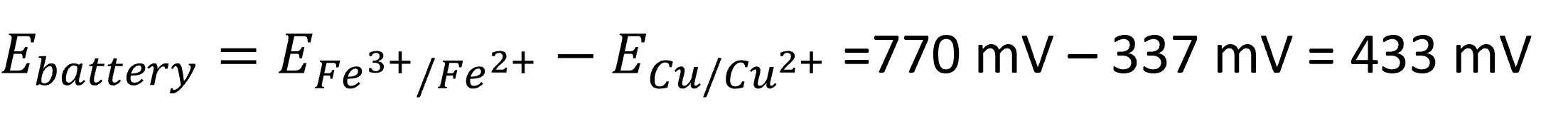Nernst equation
The Nernst equation is one of the two central equations in electrochemistry. It describes the dependency of an electrode’s potential on its chemical environment.
In more precise words: The Nernst Equation tells us what the potential of an electrode is when the electrode is surrounded by a solution containing a redox-active species with an activity of its oxidized and reduced species. The complete Nernst Equation is:
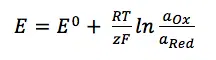
What is the E, Z, R, F and Q in the Nernst equation?
The potential is E and the activity of the reduced and oxidized species are aOx and aRed. The remaining parameters in the equation are the universal gas constant R, the temperature T, the Faraday constant F, the standard potential of the reaction Ox to Red E0, and the number of transferred electrons per molecule z.
- Nernst Equation
- The Nernst Equation tells us what the potential of an electrode is when the electrode is surrounded by a solution containing a redox-active species with an activity of its oxidized and reduced species.
It is more common to use the simplified version:
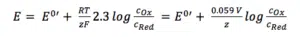
As a new parameter, the formal potential E0′ is introduced, which includes the influence of the activity coefficients.
It is essential for an electrochemist to understand that this equation works in two ways. If the potential of the electrode is changed, the solution in contact with the electrode needs to have the concentration ratio of active species indicated by the Nernst equation. To achieve this an electrochemical reaction requires to take place at the electrode.
Typical use for Nernst the equation
A typical use for Nernst equation is to calculate the potentials of two different elements and then calculate the difference between these elements to predict the potential across a cell.
For example, if a battery is to be constructed the Nernst equation can be used to predict the voltage between the two halves.
An example: Predicting battery voltage using the Nernst equation
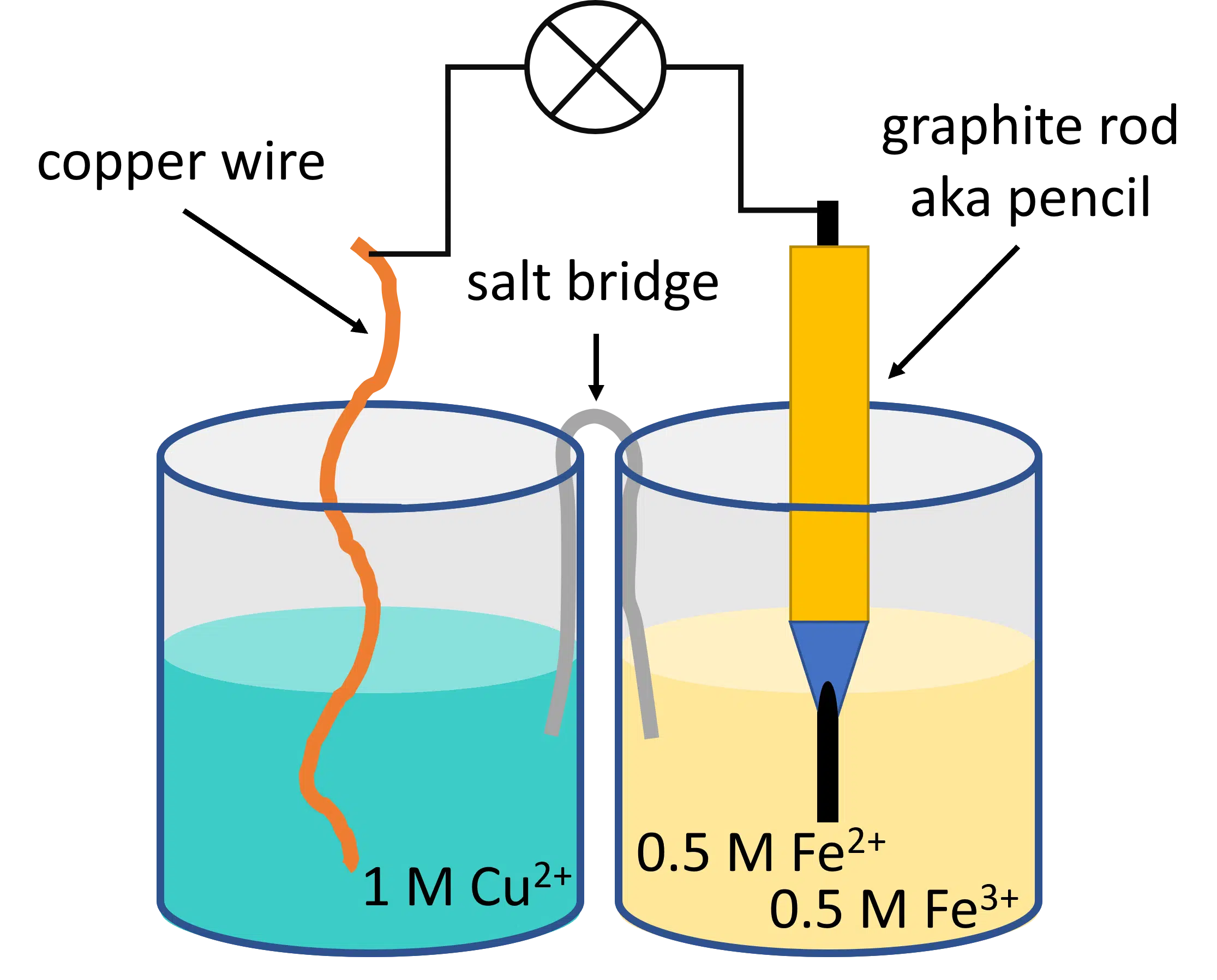
To include numbers in our example, we can use the Nernst equation to predict what voltage an improvised battery has. On the shelf, we find a 1 M CuSO4 solution and some copper wire. In a cupboard is a solution with 0.5 M FeCl3 and 0.5 M FeCl2.
-
-
- To create our battery we take two beakers and pour the iron solution into one of them and the copper solution into the other. We immerse the copper wire in the copper solution. We take a pencil and cut away the wood to expose the graphite rod. The graphite is immersed in the iron solution.
- To make a circuit the graphite rod and copper wire are connected to what we want to power. To close the circuit a piece of paper drenched with conducting solution (salt water) is used as a bridge between both beakers, with each end in of the solutions.
Figure 1 | Improvised battery - To find the battery’s voltage we need to calculate the potential difference between the two elements. The iron element should be easy.
The graphite itself is not releasing any significant amounts of ions, so we just look at the Fe(II) and Fe(III) standard potential. This is 770 mV according to Wikipedia.
- Often the formal potential E0′ is close to the standard potential E0. The oxidized species are Fe(III) and the reduced Fe(II). While calculating the electrode’s potential, there is a pleasant surprise:
A ratio of 1 leads to log 1, which is 0, and thus the complex part of the Nernst equation is just 0. The standard potential of copper(II) being reduced to copper is 337 mV according to Wikipedia. The copper wire is the reduced species. The activity of a solid body is 1. leading to:
-
Now we can calculate the potential of the battery:
And with a result of 433 mV as the maximum voltage for our battery, we realize why a copper iron ion battery isn’t used.
- To create our battery we take two beakers and pour the iron solution into one of them and the copper solution into the other. We immerse the copper wire in the copper solution. We take a pencil and cut away the wood to expose the graphite rod. The graphite is immersed in the iron solution.
Why maximum voltage?
Why did I mention here the maximum voltage? When the two elements are connected electrons will flow from the element with more cathodic potential (Cu/Cu2+ 337 mV) to the element with the more anodic potential (Fe2+/Fe3+ 770 mV).When more electrons are missing on the Cu/Cu2+ side more Cu is turned into Cu2+ to replace the electrons. Electrons arriving at the Fe2+/Fe3+ side will turn Fe3+ into Fe2+. According to the Nernst equation, the increase in Cu2+ concentration will shift the potential of the Cu/Cu2+ side to more anodic values.
While the decrease of Fe3+ concentration and increase of Fe2+ concentration will shift the potential of the Fe2+/Fe3+ side to more cathodic values. The voltage of the battery is getting lower with each electron transferred.
Goldman-Hodgkin equation
While in classic electrochemistry usually the Nernst equation is used, the Goldman-Hodgkin-Katz equation is used for the potentials across cell membranes in cell membrane physiology.
That equation doesn’t look at RedOx active species, but the charge separation due to a membrane, while taking into account the selectivity and concentration for each charged ion inside and outside the cell membrane.
- Nernst equation
- The Nernst Equation is a much used equation in electrochemistry which tells us what the potential of an electrode is when the electrode is surrounded by a solution containing a redox-active species with an activity of its oxidized and reduced species.
More information about potentiostats
More information is available in this article.
-
Articles
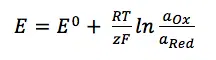
Nernst equation
The Nernst equation is one of the two central equations in electrochemistry. It describes the dependency of an electrode’s potential on its chemical environment.
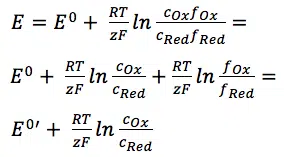
The equations behind the potentiostat
This article explains the working of a potentiostat more in depth, using Faraday’s law and the Nernst equation. For the basics of the potentiostat, please read the potentiost...
Constant Potential vs OCP or vs Reference Electrode
In this section the reasons for choosing a certain DC potential is explained. The advantages of using Ecorr as a reference point will be presented as well as how to choose in PSTrace to use potentials versus the reference electrode or versus Ecorr.
Origins of electrochemical potentials
This section is a short explanation of the processes that lead to electrochemical potential and thus to corrosion processes.